Cap. 5 Família de distribuições
Objetivos do capítulo
1. Introduzir aspectos voltados ao formato das distribuições
2. Apresentar a distribuição formal e suas características
3. Apresentar dados simulados para ilustrar a Lei dos Grandes Números e o Teorema Central do Limite
Parcialmente adaptado de Anunciação, Portugal, Landeira-Fernandez (2021). Aspectos psicométricos de instrumentos neuropsicológicos: revisão conceitual, proposta de interpretação de percentis e classificações
Em estatística, uma variável aleatória é uma função que associa cada elemento de um dado espaço amostral a um número real (\(X:\Omega \rightarrow R\)). O mapeamento desses valores depende de um experimento aleatório, seguida pela análise do conjunto de valores obtidos, chamado de realizações. Apesar desses conceitos serem importantes, o atalho pedagógico utilizado para esta definição entende as variáveis como características que podem apresentar qualquer valor, tal como peso, inteligência e renda.
Todas as variáveis apresentam resultados numéricos que, por sua vez, podem ser contínuos ou discretos. Esses valores se distribuem de acordo com uma família de distribuições de probabilidades (que também podem ser discretas ou contínuas) e podem ser pragmaticamente apresentados por uma expressão analítica (uma fórmula), tabelas ou gráficos. Em síntese, fenômenos aleatórios que podem ser representados por distribuições de probabilidades.
Os gráficos são muito úteis para indicar os três principais aspectos das distribuições, que são: a localização (ou centro), a dispersão e o formato. A tabela abaixo apresenta cada um desses componentes e uma definição.
| Componente | Definição | Medida | Gráfico |
|---|---|---|---|
| Localização | Expressa o valor médio que está sendo observado | Média, Moda e Mediana | Histograma, Boxplot |
| Dispersão | Expressa o afastamento do valor da localização | Amplitude, Variância, Desvio-padrão, IQR | Histograma, Boxplot |
| Formato | Apresenta como a variação ocorre em função da localização | Assimetria e curtose | Histograma, Boxplot |
A localização e a dispersão foram trabalhadas no capítulo sobre estatística descritiva, que também apresentou resumidamente o Coeficiente de Assimetria e Curtose. Dessa maneira, o capítulo atual tem maior ênfase sobre os possíveis formatos de uma distribuição.
Em relação ao formato, as distribuições podem ser simétricas ou assimétricas. Quando assimétricas, a assimetria pode ser à direita ou à esquerda.
Fim da versão gratuita
5.1 Distribuição simétrica
Este tipo de distribuição é simétrica em torno da média. Existem algumas famílias de probabilidade que apresentam formato similar a esse, que será melhor descrito a seguir, na seção sobre Distribuição normal.
Visualmente, a distribuição se apresenta da seguinte maneira:
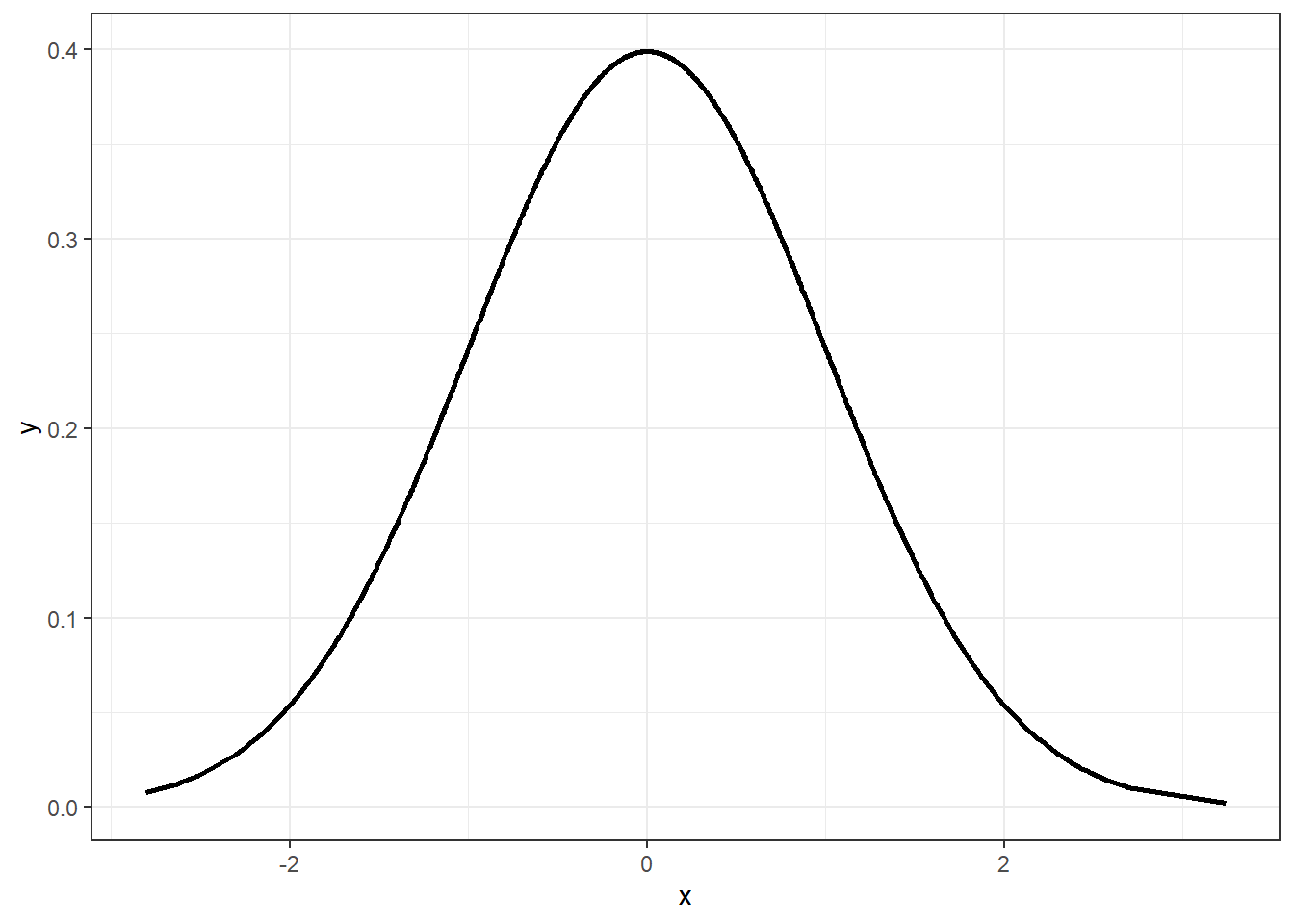
5.2 Assimetria à direita
Este tipo de assimetria é marcada por caudas longas à direita. Em distribuições que obedecem a este padrão, os outliers ou pontos anômalos tem valores significativamente altos. Visualmente, esta distribuição tem o seguinte formato.
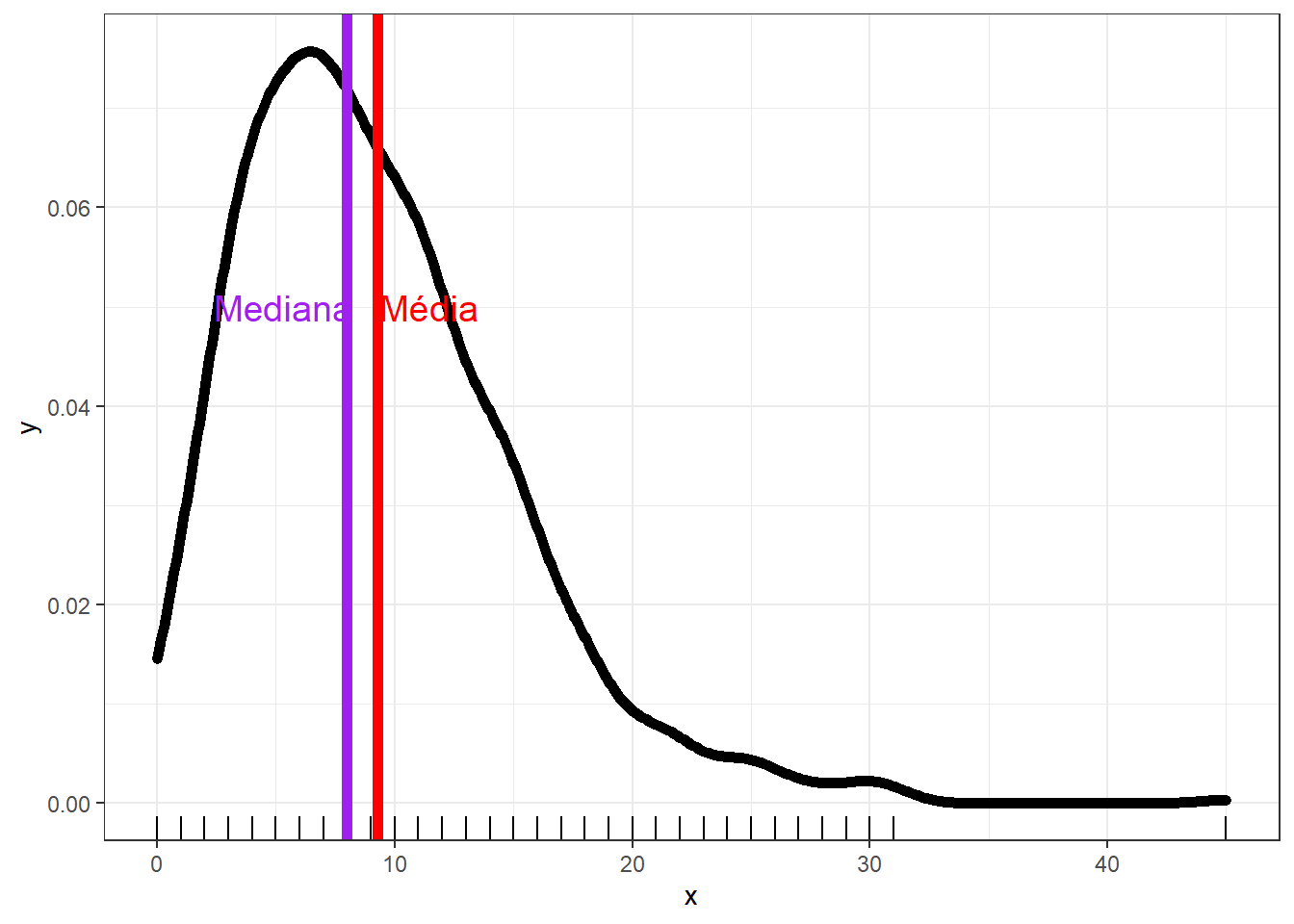
Entre as principais características, (1) a média é maior do que a mediana, (2) a quantidade de observações abaixo da média é superior à quantidade de observações acima da média e (3) o Coeficiente de Assimetria é positivo. No caso da imagem o valor é 1.1.
Entre as distribuições com este formato, estão a gamma e alguns casos particulares, como a exponencial e a qui-quadrado.
Exemplos reais: Tempo de espera em uma fila de banco, quilometragem de carros usados que estão à venda, tempo de reação em experimentos psicológicos, preço de casas à venda, número de acidentes de trânsito que uma pessoa se envolve durante um ano, quantidade de filhos que as famílias possuem.
5.3 Assimetria à esquerda (ou negativa)
Este tipo de assimetria é marcada por caudas longas à esquerda. Em distribuições que obedecem a este padrão, os outliers ou pontos anômalos tem valores significativamente baixos Visualmente, esta distribuição tem o seguinte formato.
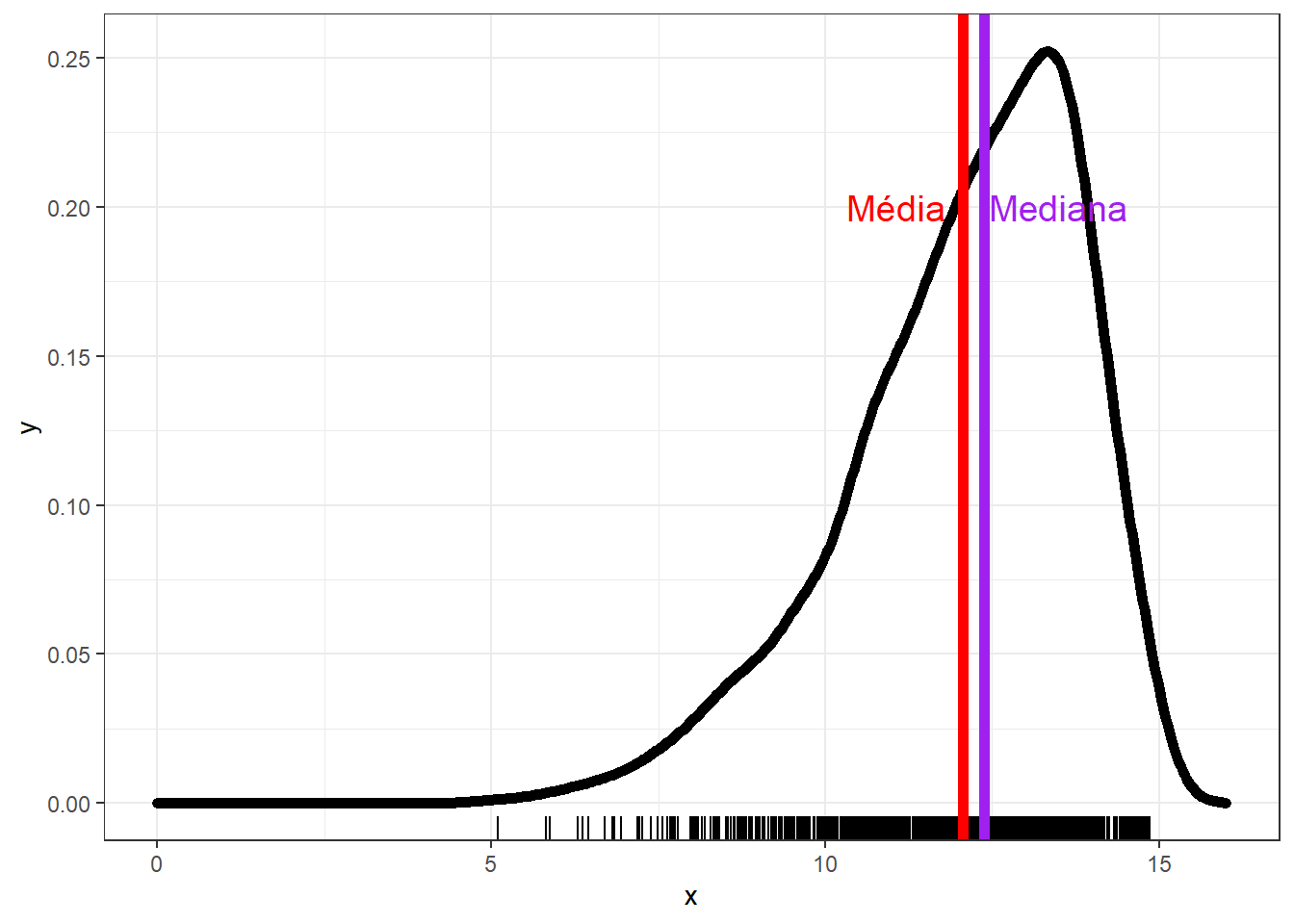
Entre as principais características, (1) a média é menor do que a mediana, (2) a quantidade de observações abaixo da média é inferior à quantidade de observações acima da média e (3) o Coeficiente de Assimetria é negativo. No caso da imagem o valor é -0.9.
Exemplos reais: Idade da morte de brasileiros, quantidade de horas que as pessoas passam na internet, quantidade de dedos que a população tem nas mãos.
5.4 A distribuição normal
A distribuição normal é um tipo de distribuição simétrica, considerada a mais importante em estatística e que apresenta características visuais e analíticas marcantes. Seu formato é apresentado a seguir:
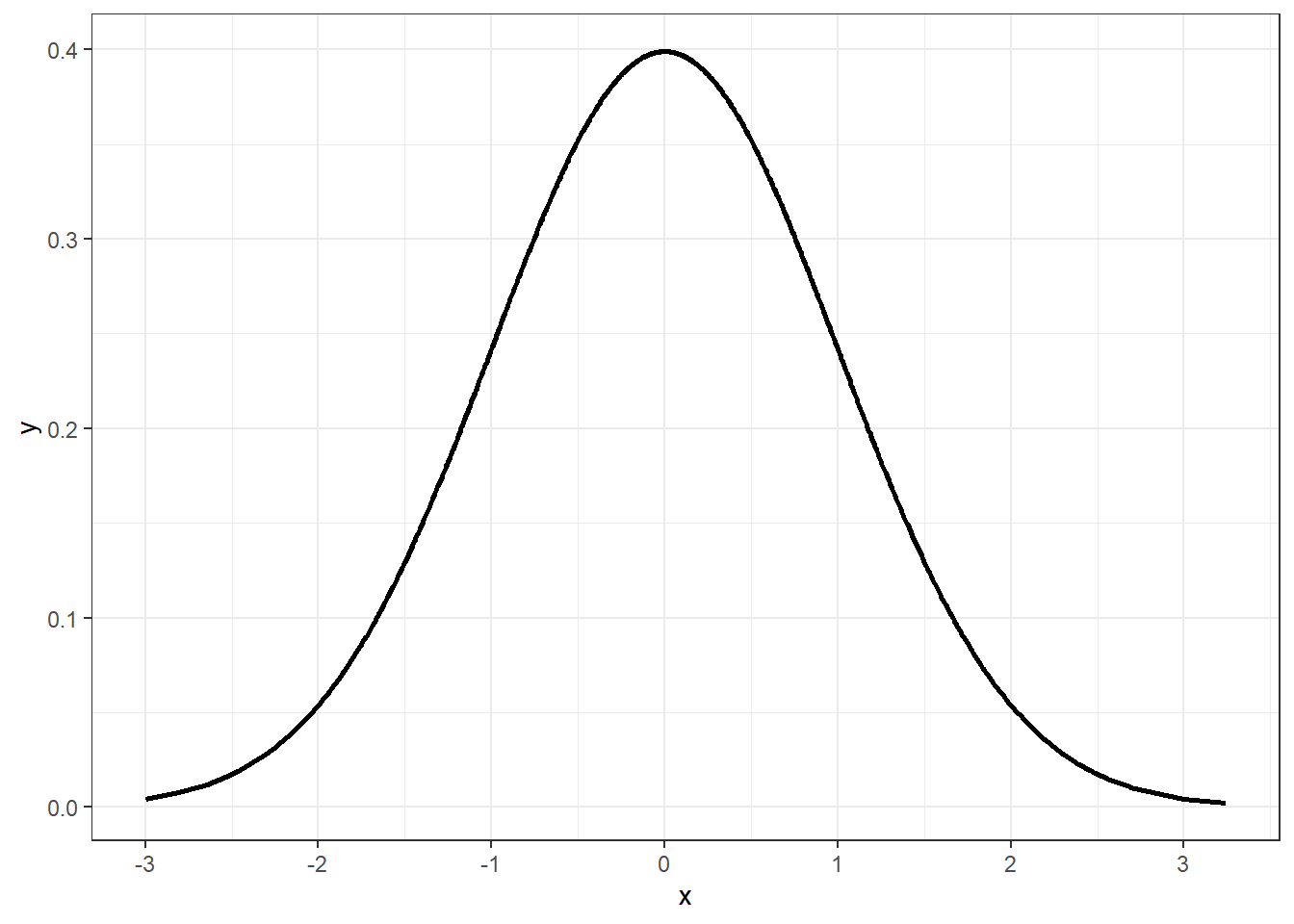
Em relação aos aspectos visuais:
- Ela é simétrica,
- Há um único pico e duas caudas, uma à esquerda e outra à direita (o que gera um formato de sino),
- Apesar de contraintuitivo, essas caudas não se estendem infinitamente à esquerda e à direita.
Em relação às características analíticas
- Ela integra a família das distribuições contínuas (e, portanto, tem uma função densidade de probabilidade),
- Ela é definida por dois parâmetros (média e variância), o que significa que é possível construir infinitas distribuições normais,
- O ponto ao centro reúne o valor da média, moda e mediana, que são iguais,
- O Coeficiente de Assimetria é igual a 0,
- O Coeficiente de Curtose é igual a 3.
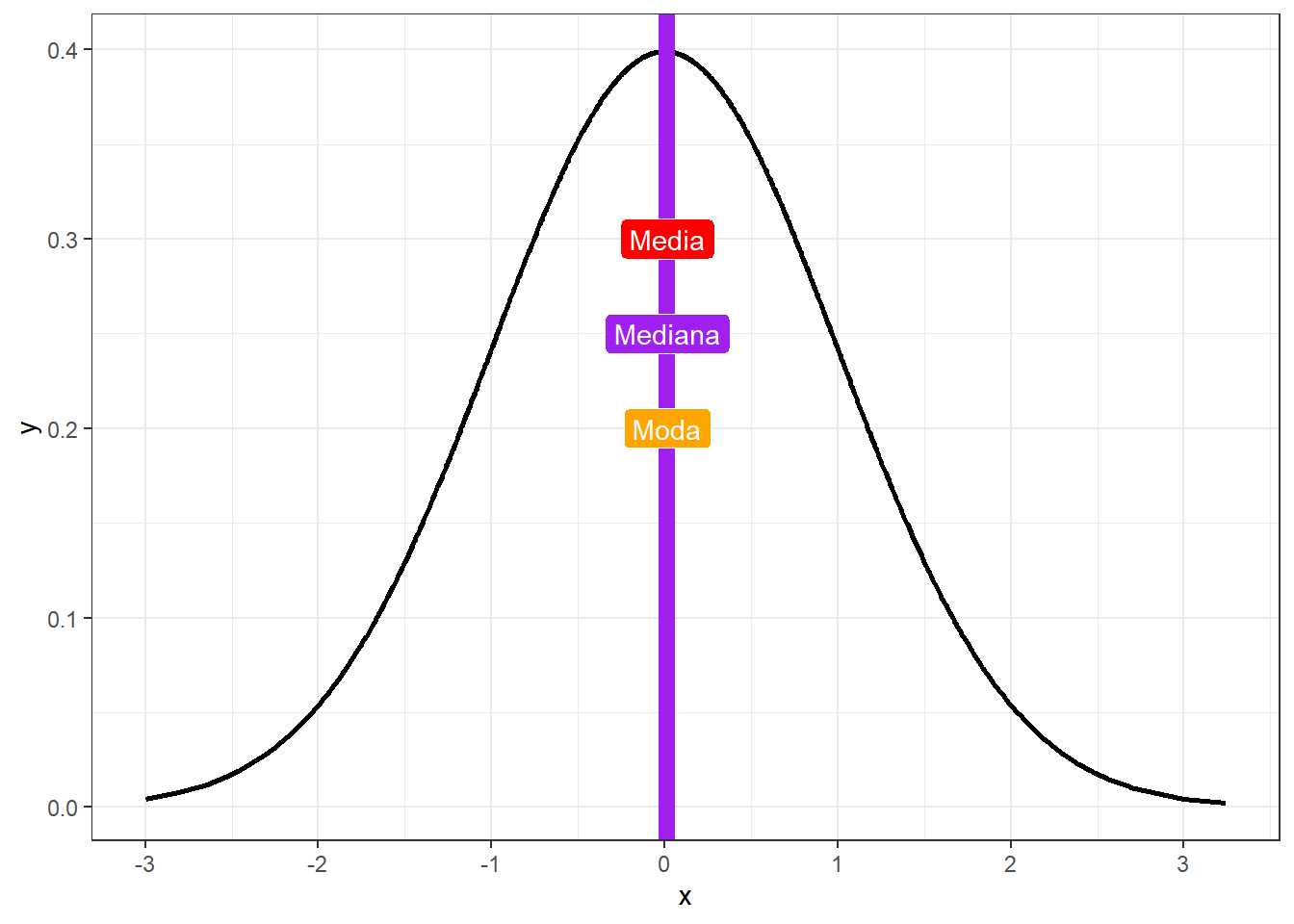
Em Psicologia, os fenômenos psicológicos são assumidos como normais, motivo pela qual essa distribuição possui ainda mais importância na área.
Exemplos reais: Altura de homens/mulheres adultos(as), erros em equipamentos de medição em astronomia, pressão arterial de adultos, tamanho de bebês recém-nascidos.
Fim da versão gratuita
5.5 A regra empírica
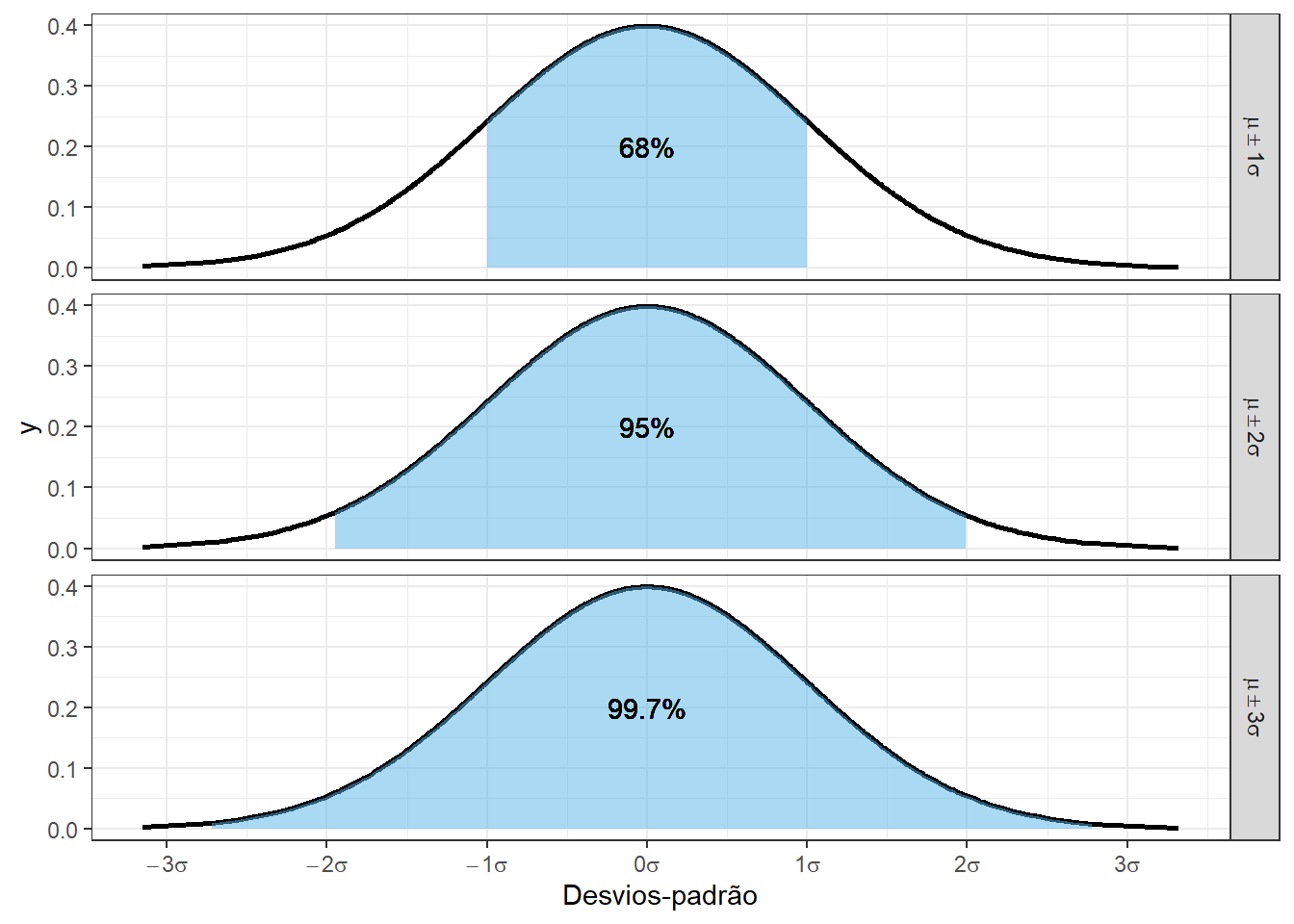
Uma característica importante da distribuição normal (e outras distribuições simétricas) é a regra empírica.
De com esta regra, em uma variável aleatória normalmente distribuída, cerca de 68% das observações estará contida no intervalo de -1 a +1 desvio-padrão, cerca de 95% das observações estará entre -2 e +2 desvios-padrão e carca de 99.7% das observações estará entre -3 e +3 desvios-padrão.
A figura abaixo apresenta esta relação.
5.6 Um resumo visual
Este capítulo pode ser entendido de muitas maneiras. Elementos visuais tendem a gerar uma assimilação mais rápida e duradoura desses conteúdos. Abaixo, há três formatos de distribuição. O cachorro no meio ilustra uma distribuição simétrica. Nela, a área embaixo da curva decai da mesma forma com referência ao centro. O cachorro da esquerda ilustra uma assimetria negativa. Repare que o rabo dele está para o lado esquerdo. Por sua vez, o cachorro da direita ilustra uma assimetria à direita. Repare que o rabo dele, por sua vez, está ao lado direito.
5.7 Importância inferencial
Uma das principais atividades realizadas na estatística é a generalização de resultados obtidos em uma pesquisa à população de onde a amostra foi retirada. Este tema será melhor apresentado no capítulo de inferência.
Atenção: A Lei dos Grandes Números e o Teorema Central do Limite são dois pilares da teoria da probabilidade e de procedimentos inferenciais.
Duas teorias em estatística são muito importantes e impactam tanto no tamanho amostral como na utilização da distribuição normal em processos inferenciais, que são a Lei dos Grandes Números (LLN) e o Teorema Central do Limite (CLT).
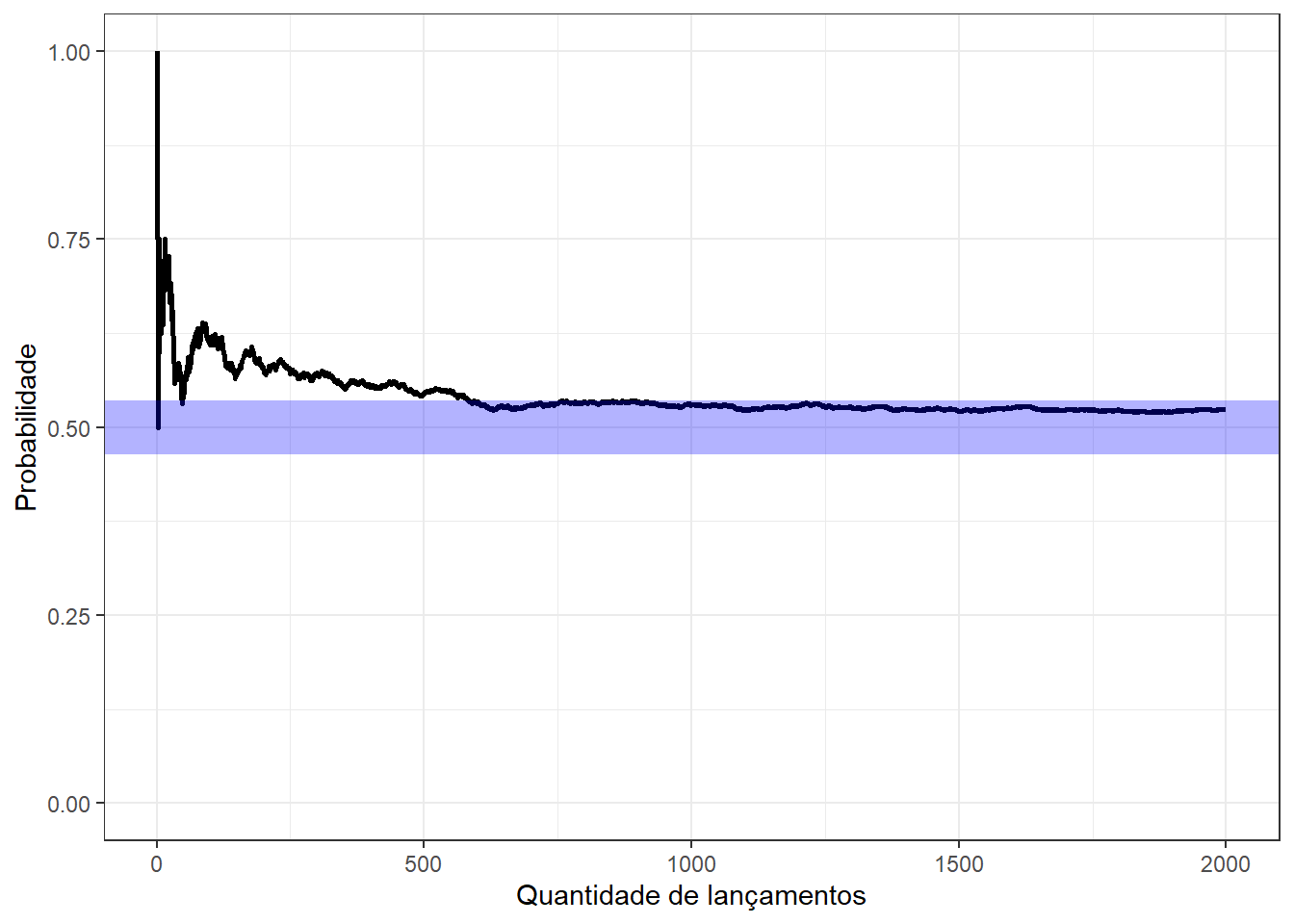
Lei dos Grandes Números (LLN): Essa Lei é um teorema fundamental da teoria da probabilidade. De acordo com ela, a média aritmética dos resultados da realização da mesma experiência repetidas vezes tende a se aproximar do valor esperado à medida que mais tentativas se sucederem. Ou seja, a média amostral converge em probabilidade à média populacional.
Uma demonstração simples é feita pelo jogo de moedas. Sabe-se que há uma probabilidade de 50% do resultado deste experimento ser cara, da mesma forma que há esta mesma probabilidade de ser coroa. É possível codificar cara como 1 e coroa como 0.
Se assumirmos que \(Sn\) o número de caras em \(n\) experimentos,há:
\[S_n = X_1 + X_2 + \dots + X_n\]
A proporção de caras é dada por:
\[R_n = \frac{S_n}{n}\]
Pela Lei dos Grandes Números, haverá uma convergência em probabilidade:
\[R_n \overset{p}{\to} p\quad quando \quad n \rightarrow \infty \] Dados simulados apresentando os primeiros resultados são:
head(lln) %>% pander::pander()| lancamento | resultado | acumulado_caras | prob_caras |
|---|---|---|---|
| 1 | Cara | 1 | 100 |
| 2 | Coroa | 1 | 50 |
| 3 | Cara | 2 | 66.67 |
| 4 | Cara | 3 | 75 |
| 5 | Coroa | 3 | 60 |
| 6 | Cara | 4 | 66.67 |
À medida que a quantidade de lançamentos aumenta, a probabilidade se aproxima à esperada, ilustrando a Lei dos Grandes Números. O gráfico a seguir demonstra esse resultado.
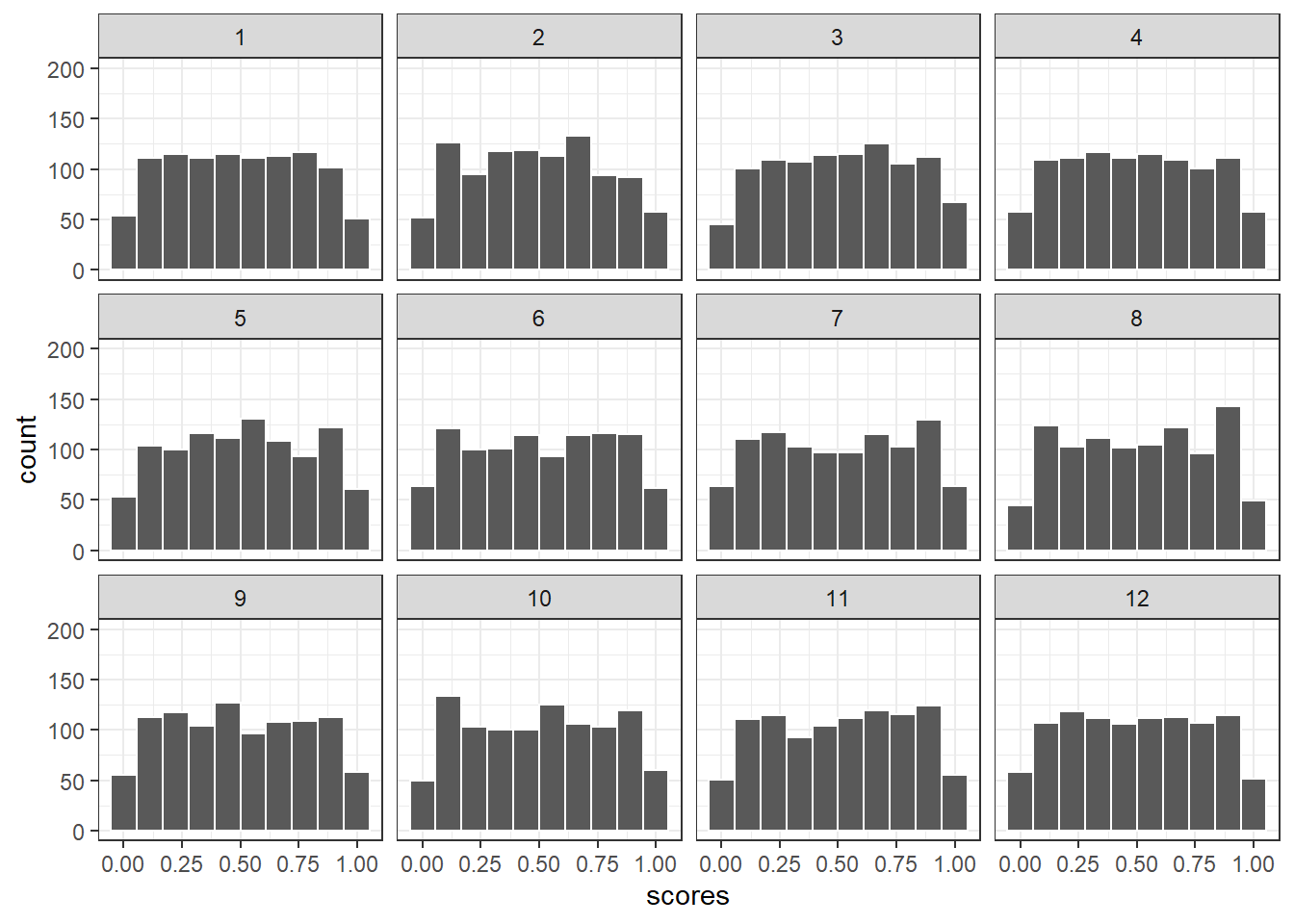
O Teorema Central do Limite (CLT): Se uma variável aleatória (por exemplo, X) puder ser representada pela soma de quaisquer \(n\) variáveis aleatórias independentes, que satisfaçam certas condições gerais, esta soma terá distribuição aproximadamente normal para \(n\) suficientemente grande.
Uma demonstração pode ser feita. Se um conjunto de pesquisas forem realizadas em uma variável cuja distribuição tenha formato uniforme, em cada uma das pesquisas (realizações), os resultados terão formato uniforme, tal como demonstrado a seguir:
Caso a média de cada uma das pesquisas (realizações) seja tirada e arquivada em um banco de dados, os 10 primeiros resultados serão os seguintes:
head(clt_sample_means) %>% pander::pander()| samples | means |
|---|---|
| 1 | 0.496 |
| 2 | 0.4917 |
| 3 | 0.5188 |
| 4 | 0.4968 |
| 5 | 0.5075 |
| 6 | 0.5008 |
A distribuição das médias das médias é, aproximadamente, normal.
ggplot(clt_sample_means, aes(x=means))+
geom_histogram(color="white", bins=15)+
theme_classic()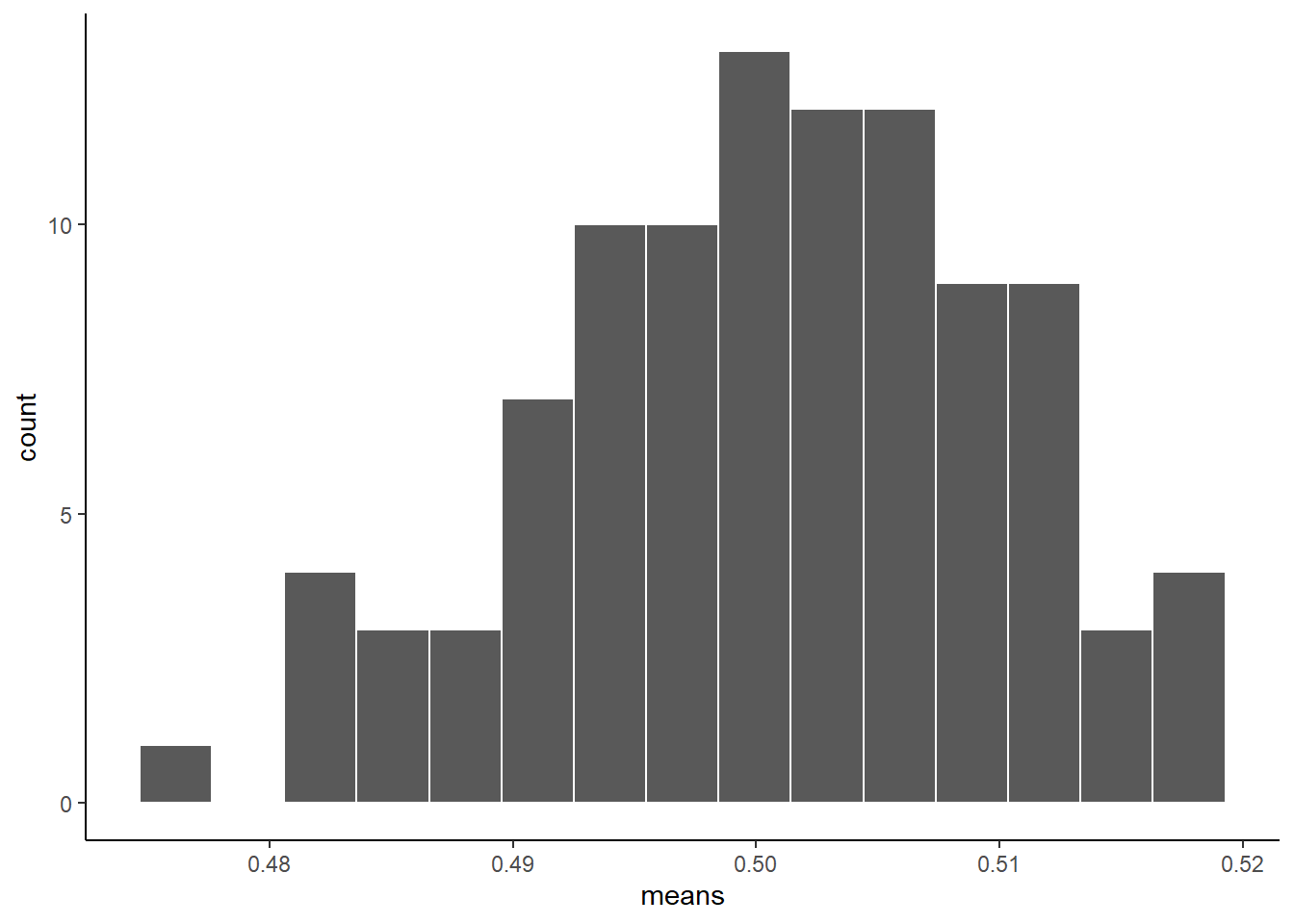
5.8 Resumo
Este capítulo introduziu aspectos relacionados ao formato da distribuição das variáveis, com os seguintes pontos principais:
- Todas as variáveis se distribuem e o formato delas pode ser descrito de maneira analítica, tabular ou gráfica
- De maneira sintética, as distribuições podem ser simétricas ou assimétricas
- A assimetria à direita é também chamada de positiva
- A assimetria à esquerda é também chamada de negativa
- A distribuição normal é a mais importante em estatística e muito utilizada em Psicologia
- A Lei dos Grandes Números e o Teorema Central do Limite são fundamentais em aspectos inferenciais
Este livro pode ser adquirido no site da Amazon, clicando aqui.
Ao comprar a obra, você auxilia este projeto e ajuda a execução de novos. Qualquer dúvida, entre em contato por luisfca@puc-rio.br
Este livro pode ser adquirido no site da Amazon, clicando aqui.
Ao comprar a obra, você auxilia este projeto e ajuda a execução de novos. Qualquer dúvida, entre em contato por luisfca@puc-rio.br